Karp's 21 Problems (S)
| 392219 | Wittler, Kobert | Summer 2024 | Wednesday 10:15-11:45 | U10-146 |
(Je nach Wunsch/Bedarf der Studierenden wird das Seminar auf Deutsch oder Englisch durchgeführt.
Depending on the wishes/demands of the students, this seminar can be held in English or German.)
Based on a classical research paper, the participants will give oral presentations and write short summaries about algorithmic problems and their complexity. Formal problems / algorithmic solutions will be discussed and, as a practical exercise, implemented in a proof-of-concept fashion. Talks and essays can be done in German or English. The first day covers an introduction into the topic and an overview of possible topics, which will then be distributed to the students. Aspects of scientific writing and presenting will be covered as well.
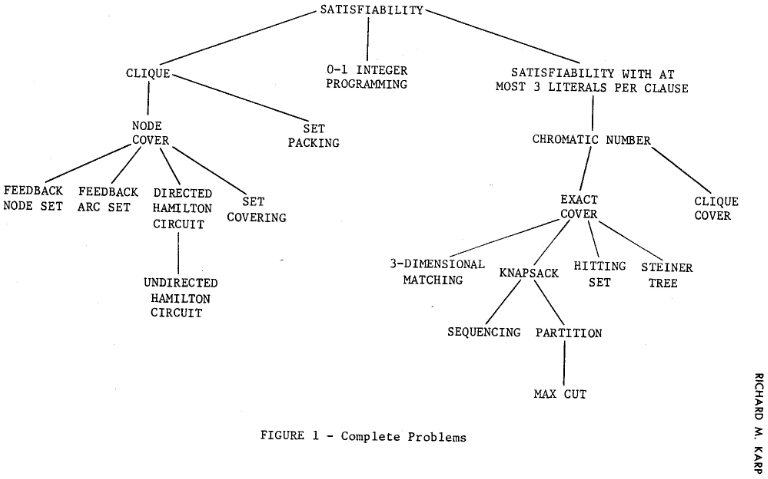
The overarching topic of this semester are “Karp's 21 NP-complete problems”: Richard M. Karp. "Reducibility among combinatorial problems" (1972)
In this work, Karp shows NP-hardness of many classical, important formal problems, mainly by listing reductions/equivalence between them. The given reductions appear like brief cooking recipes, but no intuition or proof of equivalence is provided. The relations are not too obvious but also not too hard to see – excellent exercises for understanding formal statements, logical thinking, formal writing etc.
In the first sessions, we will give a reminder on NP-completeness, discuss the paper by Karp in general, show an exemplary NP-completeness proof, and also cover aspects of scientific presentations and writing.
Each participant will be responsible for one problem (say A) and in particular its reduction from another NP-complete problem (say B), understand it and explain it to the others. We will pre-select a list of appropriate problems and provide help where necessary.
Concrete tasks are:
- Carefully read the original publication of Karp until 17 April
- Understand the two problems (A and B)
- Understand the reduction from B to A
- A presentation and written essay comprising:
- motivation for / relevancy of problem A
- formal definition of both problems
- NP-completeness proof for A (mainly the reduction from B)
- example for the reduction
- research on approximations, heuristics, problem variants
- A (naive) implementation including a stress test (How far can we get with this?)
The following problems will be covered:
- Set Packing (from Clique)
- Exact Cover (from Chromatic Number)
- Partition (from Knapsack)
- Steiner Tree (from Exact Cover)
As backup, we could also do:
- Feedback Arc Set (from Node Cover)
- Hitting Set (from Exact Cover)
- Knapsack (from Exact Cover)
- Sequencing (from Knapsack)
| Day | Topic | Responsible person |
|---|---|---|
| 10.04. | Overview | all |
| 17.04. | Discussion of Karp's Paper | all |
| Repetition NP-completeness | Roland (slides) | |
| Example: Clique (from Satisfiability) | Kassian | |
| 24.04. | Scientific writing & presentations | Roland Slides: HowToRead chatGPT: Beautifully phrased nonsense |
| 01.05. | – (national holiday) | |
| 08.05. | ||
| 15.05. | ||
| 22.05. | Set Packing | Olivia (Kassian) |
| 29.05. | ||
| 05.06. | ||
| 12.06. | Exact Cover | Enna (Roland) |
| 19.06. | ||
| 26.06. | Partition | Asal (Kassian) |
| 03.07. | Abgabe Implementierung | |
| 10.07. | presentation of implementations | all |
| 17.07. | ||

